Khi đang học tập hay nghiên cứu về toán học, khoa học dữ liệu hay kinh tế học, chắc hẳn bạn đã từng nghe qua thuật ngữ “local maximum”. Nhưng đó là gì? Trong bài viết này, chúng ta sẽ cùng tìm hiểu khái niệm local maximum và ứng dụng của nó trong thực tế.

Định nghĩa local maximum

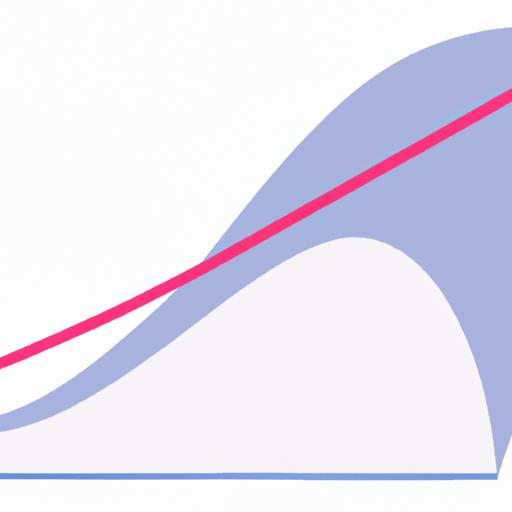
Local maximum là một giá trị cực đại (lớn nhất) trong một khu vực nhất định của một hàm số. Nó là một điểm nằm trên đỉnh của một đồ thị và có giá trị lớn hơn hoặc bằng tất cả các giá trị khác trong khu vực lân cận.

Ví dụ, hãy tưởng tượng một đường cong trên một đồ thị, local maximum của đường cong là điểm cao nhất trong một khoảng thời gian nhất định, nhưng không cần phải là điểm cao nhất trên toàn bộ đường cong.

Ví dụ minh họa

Để hiểu rõ hơn về khái niệm local maximum, hãy xem xét ví dụ sau.

Giả sử bạn đang xây dựng một chiếc máy tính để phân tích dữ liệu về giá cổ phiếu của một công ty. Sau khi thu thập và xử lý dữ liệu, bạn tạo ra một đồ thị thể hiện giá cổ phiếu theo thời gian.

Trên đồ thị này, local maximum có thể được định nghĩa là giá cổ phiếu cao nhất trong một khoảng thời gian nhất định. Nhưng nếu bạn xem xét toàn bộ đồ thị, giá cổ phiếu có thể có giá trị cao hơn.

Trong phần tiếp theo của bài viết, chúng ta sẽ tìm hiểu thêm về các thuật ngữ liên quan đến local maximum.

Các Thuật Ngữ Liên Quan Đến Local Maximum

Khi nói đến local maximum, chúng ta cũng không thể không đề cập đến các thuật ngữ khác liên quan, bao gồm global maximum, local minimum và global minimum.

Global Maximum

Trong toán học, global maximum là giá trị lớn nhất của một hàm số trên toàn bộ miền xác định. Nó là giá trị lớn nhất của hàm số và không bị giới hạn bởi bất kỳ điều kiện nào. Ví dụ, nếu bạn xét hàm số f(x) = x^2 trên miền xác định [-1, 1], global maximum của hàm số này là 1 tại x = 1.

Local Minimum

Tương tự như local maximum, local minimum là giá trị nhỏ nhất của một hàm số trong một khu vực nhất định. Nó là một điểm nằm dưới đáy của một đồ thị và có giá trị nhỏ hơn hoặc bằng tất cả các giá trị khác trong khu vực lân cận.

Global Minimum

Global minimum là giá trị nhỏ nhất của một hàm số trên toàn bộ miền xác định. Nó là giá trị nhỏ nhất của hàm số và không bị giới hạn bởi bất kỳ điều kiện nào. Ví dụ, nếu bạn xét hàm số f(x) = x^2 trên miền xác định [-1, 1], global minimum của hàm số này là 0 tại x = 0.

Tìm hiểu các thuật ngữ này sẽ giúp bạn hiểu rõ hơn về khái niệm local maximum và đồng thời có thể áp dụng chúng trong các lĩnh vực khác nhau. Trong phần tiếp theo của bài viết, chúng ta sẽ đi sâu hơn vào các ứng dụng của local maximum.

Công Dụng Của Local Maximum Trong Các Lĩnh Vực Khác Nhau

Local maximum là một khái niệm quan trọng và được ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau. Dưới đây là một số ứng dụng của local maximum trong các lĩnh vực khác nhau.

Toán Học

Trong toán học, local maximum được sử dụng để xác định giá trị lớn nhất của một hàm số trong một khoảng xác định. Điều này giúp cho các nhà toán học có thể giải quyết các bài toán phức tạp trong đại số, hình học và tính toán.

Khoa Học Dữ Liệu

Trong khoa học dữ liệu, local maximum được sử dụng để tìm kiếm giá trị cao nhất của một hàm số trong một tập dữ liệu. Điều này giúp cho các nhà khoa học dữ liệu có thể phân tích và dự đoán xu hướng của dữ liệu trong tương lai, từ đó đưa ra quyết định và kế hoạch phù hợp.

Kinh Tế Học

Trong kinh tế học, local maximum được sử dụng để tìm kiếm giá trị lớn nhất của một hàm số trong các tình huống khác nhau, chẳng hạn như giá cổ phiếu, giá trị tài sản, lợi nhuận, và nhiều hơn nữa. Việc tìm kiếm local maximum giúp cho các nhà kinh tế có thể đưa ra những quyết định đúng đắn và tối ưu hóa lợi nhuận của doanh nghiệp.

Tóm lại, local maximum là một khái niệm quan trọng trong nhiều lĩnh vực khác nhau, giúp cho người sử dụng có thể tìm kiếm giá trị lớn nhất của một hàm số trong một tập dữ liệu. Việc tìm kiếm local maximum giúp cho người sử dụng có thể đưa ra những quyết định đúng đắn và tối ưu hóa lợi nhuận của doanh nghiệp.

Các phương pháp tìm kiếm local maximum

Khi phân tích dữ liệu hoặc tối ưu hóa hàm số, việc tìm kiếm local maximum là một vấn đề quan trọng. Tuy nhiên, việc tìm kiếm local maximum không phải lúc nào cũng dễ dàng. Có nhiều phương pháp để tìm kiếm local maximum, dưới đây là một số phương pháp phổ biến:

Gradient descent

Gradient descent là một phương pháp tối ưu đơn giản và phổ biến để tìm kiếm local maximum. Phương pháp này sử dụng đạo hàm của hàm số để xác định hướng đi tối ưu nhất. Khi đạo hàm bằng 0, ta sẽ tìm được local maximum.

Tuy nhiên, gradient descent có một số nhược điểm như cần chọn tỉ lệ học tốt và dễ bị rơi vào local minimum.

Newton’s method

Newton’s method là một phương pháp tìm kiếm local maximum sử dụng đạo hàm và đạo hàm bậc hai của hàm số. Phương pháp này có thể tìm được local maximum nhanh hơn so với gradient descent, nhưng lại cần tính toán đạo hàm bậc ha

Quasi-Newton methods

Quasi-Newton methods là một loại phương pháp tối ưu sử dụng đạo hàm của hàm số để tìm kiếm local maximum. Phương pháp này khá linh hoạt và dựa trên bản chất của Newton’s method, nhưng không cần phải tính toán đạo hàm bậc ha
Tuy nhiên, cũng giống như các phương pháp tìm kiếm local maximum khác, quasi-Newton methods cũng có nhược điểm là dễ bị rơi vào local minimum nếu không chọn cẩn thận tham số.

Như vậy, tìm kiếm local maximum là một vấn đề quan trọng trong việc tối ưu và phân tích dữ liệu. Việc sử dụng các phương pháp tìm kiếm local maximum phù hợp sẽ giúp cho quá trình tối ưu và phân tích dữ liệu có hiệu quả hơn.

Ưu điểm và nhược điểm của local maximum

Ưu điểm

Local maximum là một khái niệm quan trọng và có nhiều ứng dụng trong khoa học và kinh tế. Các ưu điểm của local maximum bao gồm:

• Là một công cụ hữu ích để giải quyết các vấn đề tối ưu hóa trong nhiều lĩnh vực khác nhau.
• Giúp tối ưu hóa các chương trình máy tính và chuỗi sản xuất.
• Có thể sử dụng trong các phương pháp dự đoán và mô hình hóa để tìm ra các giá trị tối ưu.

Nhược điểm

Tuy nhiên, như mọi khái niệm khác, local maximum cũng có nhược điểm của riêng nó. Những nhược điểm này bao gồm:

• Không phải lúc nào local maximum cũng là giá trị tối ưu nhất trên toàn bộ đồ thị.
• Việc tìm kiếm local maximum có thể rất khó khăn và tốn nhiều thời gian.
• Có thể dẫn đến các vấn đề về tối ưu hóa giá trị.

Tóm lại, local maximum là một khái niệm quan trọng trong nhiều lĩnh vực và có nhiều ưu và nhược điểm. Chúng ta cần hiểu rõ về khái niệm này để áp dụng hiệu quả trong thực tế.

Kết luận

Như vậy, trong bài viết này, chúng ta đã tìm hiểu khái niệm local maximum và các ứng dụng của nó trong thực tế. Chúng ta đã biết được rằng local maximum là một giá trị cực đại trong một khu vực nhất định của một hàm số, có giá trị lớn hơn hoặc bằng tất cả các giá trị khác trong khu vực lân cận.

Chúng ta cũng đã tìm hiểu thêm về các thuật ngữ liên quan đến local maximum như global maximum, local minimum và global minimum. Bên cạnh đó, chúng ta cũng đã tìm hiểu các phương pháp tìm kiếm local maximum như gradient descent, Newton’s method và Quasi-Newton methods.

Local maximum là một khái niệm quan trọng trong các lĩnh vực như toán học, khoa học dữ liệu hay kinh tế học. Việc hiểu rõ khái niệm này sẽ giúp chúng ta áp dụng tốt hơn trong thực tế và đạt được kết quả cao hơn.

Nếu bạn cần thêm thông tin chi tiết hoặc có bất kỳ thắc mắc nào về local maximum, hãy để lại bình luận bên dướChúng tôi sẽ cố gắng giải đáp mọi thắc mắc của bạn.

Trân trọng,

hefc.edu.vn